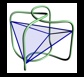
Schematic of 286 intersection wire diamond
The wire diamond is a model of the structure of diamond. A diamond is made up of carbon atoms. Each carbon atom has bonds to four neighbouring carbon atoms. Each straight length of wire represents such a bond, and the intersections where four of such bonds meet represents a carbon atom.
The eight outside faces of the wire diamond are the primary cleavage planes that diamond cutters use in shaping rough diamonds. They cut on other planes as well to form a gem, but since these are the primary planes, the silhouette of the wire diamond has always been the two-dimensional shape associated with the name 'diamond'.
The wire diamond is constructed by hanging wire zig-zags, one beneath the other. This way of creating the diamond structure is original and patentable. We have chosen not to patent it, but by publishing a booklet, and this webpage, we prevent others from patenting it, allowing anyone to make it without worrying about patent violation. (Or you could buy one from me).
84 intersection Wire Diamond
It is possible to consider the wire diamond as a work of art. Viewing it in different directions provides various attractive patterns. It lives up to the perfection and elegance we expect of a diamond.
Another possible use of the wire diamond is as a three-dimensional frame on which to play games, analogous to a two-dimensional game board. It was originally created in 1999 in response to a request by Walt McKibben (now deceased) to explore possible ways of playing the game Go in three dimensions. It serves this function very well, with points on the interior having four neighbours, corner points having two, and edge/side points having three. This is the same on the two-dimensional board and the wire diamond.
More information
- The Games - some ideas for games to play on the diamond structure.
- More pictures - other photographs of the diamond board.
- Ordering Information - how to buy a diamond board from me.
- Miscellaneous - including links to programs for playing diamond go virtually.
- General Graph Go - for if moving to diamond structure just isn't enough generality.
- Topological Go - for if moving to general graphs just isn't enough generality.
Acknowledgements
- Walt McKibben - realised the possibilities of 3-D Go
- Ephraim Segerman - hanging wire diamond idea, D-space, technical/mathematical advice, money
- Djilda Segerman - origami 'diamond' stones
- Steve Tickle - dot matrix printing to pre-stress paper for folding
- Peter Harvey - other games ideas
More Pictures
The smallest live group. It uses a corner of the octahedron and seven stones. Interestingly there are three disjoint strings of stones, each of which touches both eyes.
The pattern in another view. There are many nice symmetries of diamond structure that appear when viewed from a particular direction.
Something to hang it from. The wire diamond is essentially a mobile and holds together with gravity only, so it needs to be supported from above.
Would you believe, a ko. These are hard enough to see in real life 3D with stereoscopic vision...