- Diamond Go
- Diamond Halma (or Chinese Chequers)
- Diamond Chequers (or Draughts)
- Peter Harvey's Diamond Chess
- Eph's Diamond Chess Concept
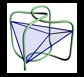
The principal reason for creating the wire diamond was to convert Go (and other games) from 2-D to 3-D, while reserving the feature of the standard 2-D board: each intersection has four neighbours. This allows many games to be converted, hopefully adding to them in the extra dimension, rather than changing them out of recognition to make the game work. Other, similar ideas, (eg. 3-D Tic-Tac-Toe) have concentrated on a system of cubes, perhaps made from perspex. This has the disadvantage of distorting the 'perfection' of an orthogonal array or cubic array (the usual coordinates system for plotting points in 3-D: just stacked cubes) because of problems such as hand space and cost. Also, the interaction on a small scale between pieces is very different because of the extra neighbours from any point (on a 2-D grid, if you were a queen in chess, you could go in one of eight directions from any point: if it were a 3-D cube array, you could go in twenty six). In moving along a diamond lattice (hereafter referred to as 'D-Space') however, there are still four neighbours, although working with 'diagonals' becomes far more difficult. The other problem is that there are no straight lines for chess pieces to run along, although it is possible with a little imagination.
Since the idea of such a gaming diamond is new, most of these games haven't had even preliminarily rules set down, let alone play tested: try them out and see if they work, alter any rules as you see fit. Any suggestions and new ideas for games or improvements for those below are welcome. The main difference between D-Space and a traditional 2-D grid is that the possible routes to take increases more rapidly because there are fewer duplications. On a 2-D grid, you can be back where you started after taking four, or three steps, including diagonals, without retracing steps, but in D-Space you need to go six. Another distinction is that the ratio of total intersections to edge intersections is different: there are more edge connections on the wire diamond than on a 2-D grid of similar magnitude. These differences become more important in games such as Go.
If anyone comes up with an idea for a game to play on the diamond, or has any comments, email me with it and I'll put it up.
Diamond Go
This game is played in exactly the same way as the 2-D game. Apart from the extra difficulty of seeing the overall view of the game, the differences become apparent in the tactics. Basically, it is more difficult to surround a string of stones (because there are more possible routes through D-Space), but it is also more difficult to defend, and more difficult to create eyes. This means that the extra edges (or sides) become very important for defence (and attack for that matter). Fundamentally, it is a different game. The tactics and stock plays have not yet been worked out, so we cannot really pass judgment on it in comparison with 2-D Go, but it is an interesting game.
Diamond Halma (or Chinese Chequers)
The aim of the game is to get your pieces from one corner of the wire diamond to the other, while the other player(s) are trying to do the same. Set your pieces up in the thirteen or so (depending on the size of diamond) last intersections nearest your corner. If playing with two people, your opponent sets up on the opposite corner, if with three, set up on perpendicular corners (someone going vertical) etc. Up to six could play, although the more there are playing, the less effective planning ahead can be, and the more opportunistic the game becomes.
Players take turns and may move one piece in one of two ways. Either, move one intersection in any direction, and stop, or jump over another piece to land on the other side of them, and you can carry on jumping over more pieces, changing direction, and even tracing back steps, until there is no one else to jump over. You can jump over your own, and other peoples pieces, and no one is ever taken.
The main difference, apart from the extra routes to take, is in the process of jumping. On the 2-D grid, it is obvious to see in which square you land in after jumping someone: just trace a line through you and them. In D-Space, after going over someone, there are three possible places to land, all at the same angle so there is no 'right' choice. The solution is to be able to land in any of the three intersections. This makes the game rather chaotic, and very quick, but again, the relative merits and disadvantages of this twist in the rules are not known.
Diamond Chequers (or Draughts)
This is played very similarly to Diamond Halma, with a similar set up. The differences are that you have only two options as to where to land after taking a piece (as you cannot go backwards), until you become a king, in which case, as in Diamond Halma, there would be three options. Otherwise, it is played just as normal draughts.
Peter Harvey's Diamond Chess
Converting a game such as chess to the wire diamond is not easy. For a start, there are no clearly defined straight lines for pieces such as queens, also, the mechanism for checkmate could require many pieces to stop all exits for a king. This version of diamond chess keeps the ideas of the power hierarchy and territorial conquest, but instead of working with infinite movement in one direction, uses ranged movement in any direction. The two sides start in opposite corners, a plane of twelve or sixteen pawns in front of the other pieces. Kings, as in normal chess move one in any direction. Each pawn can only move forward one intersection, but has two options at each stage. They take the same way that they move (?). Thus a stand off similar to normal chess would develop as anyone moving can be taken (unless you are backed up, leading to an exchange). Bishops can move only two intersections, not more or less, so effectively jump across an angle of a hexagon (should a piece in the way be able to block a bishop moving in this way?). This means that the two bishops on different sets of intersections, as in normal chess, may never meet. Queens can move one, two, or four intersections, which gives them considerable power. Knights may only move three intersections, which again gives them a unique power. Provision for rooks is not as easy. The point of rooks in normal chess is to act as long range threatening pieces, for both attack and defence. This is not easy to simulate in a fashion similar to the rest of the game. A possible way would be to have rooks purely as defensive pieces, confined to a plane perpendicular to the direction of the pawns, but allowed to move like a bishop but any distance in a straight line. (Ed: this wouldn't make much sense unless you have the diamond in front of you.)
Distinguishing between pieces should not be a problem. With only a few non-pawns, a painted letter or similar should do.
Eph's Diamond Chess Concept
There may be no straight lines in D-space, but there are six directions of straight zig-zags, like the wire pieces used in constructing the wire diamond. There are the two horizontal directions along the wire zig-zags used in construction, and there are two new directions of zig-zags that can be seen along the faces of the wire diamond on each side of any one of the four horizontal edges half-way down the structure.
The wire zig-zags on two of those horizontal edges on opposite sides of the diamond are where the power pieces (ie not pawns) are positioned at the start of the game, and where pawns can be queened. Initially, pawns are placed to block access to that zig-zag from all others..
The direct path between the two opponents involves a zig-zag direction going straight across between them. Pawns advance in this direction. The other horizontal zig-zag direction, perpendicular to this one, offers no advance towards one's opponent. Pawns capture in this direction. Rooks can travel any unobstructed distance along one of these two zig-zag directions in one move. Since one of them can stop on a point at the top or bottom of a zig-zag, an alternation of movements in the two directions can raise or lower the horizontal level on which it operates.
Bishops can travel any unobstructed distance along any one of the other four (ie non-horizontal) zig-zag directions, and queens can travel either as bishops or as rooks. The movements of the king and of the knights are also analogous to what they do in the normal two-dimensional game. A wire diamond with 165 intersections (and two queens per side) is recommended.